The formula to calculate friction when raising a load is:
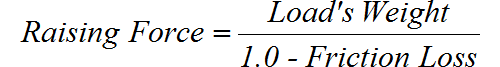
This illustration shows the same system that was used to calculate friction when lowering through a pulley, but this time the load is being raised. Using the above formula, you can see that you must pull 111 kilograms to raise the 100-kilogram load. The pulley's friction requires us to pull an extra 11 kilograms.

This illustration shows the same system that was used to calculate friction when lowering through a brake bar rack with 90% friction, but this time we are trying to raise the load (a dumb thing to try, but it's a good example of friction).
When lowering, the 90% friction reduced the forces from 200 pounds to 20 pounds. As shown in the following formula, if you tried to raise the load through the rack you would have to pull a whopping 2,000 pounds.
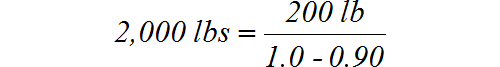
In the basic 3:1 raising system shown here, you would expect to pull 67 pounds to raise the 200-pound load (i.e., one-third of the 200 pounds). However, if each of these pulleys induces 10% friction, then your pulling team will need to pull ~74 pounds to raise the load. In effect you have a 2.7-to-1 system.
If you increase the friction in the pulleys to 20%—a not-unreasonable value for smaller pulleys—you will need to pull 82 pounds to raise your 200-pound load. Your 3:1 system is now only providing a 2.4:1 mechanical advantage. The pulleys' 20% fiction add 15 pounds to the 67 pounds you expected.
This table shows the actual mechanical advantage of 2:1, 3:1, and 5:1 systems based on the friction in the pulleys. For example, if the pulleys in a 5:1 system each have 15% friction, you will effectively have a 3.75:1 system rather than a 5:1. (This table does not include change of direction pulleys which would further decrease the mechanical advantage.)
| Friction | 2:1 | 3:1 | 5:1 |
|---|---|---|---|
| 0% | 2:00:1 | 3.00:1 | 5.00:1 |
| 5% | 1.95:1 | 2.85:1 | 4.55:1 |
| 10% | 1.90:1 | 2.70:1 | 4.15:1 |
| 15% | 1.85:1 | 2.55:1 | 3.75:1 |
| 20% | 1.80:1 | 2.45:1 | 3.40:1 |
| 30% | 1.70:1 | 2.20:1 | 2.70:1 |
| 40% | 1.60:1 | 1.95:1 | 2.15:1 |
| 50% | 1.50:1 | 1.75:1 | 1.60:1 |
It is intuitive that friction increases forces when raising and that minimizing friction in pulleys is a good idea, but there may be times when you do not have low-friction pulleys and you are forced to use lesser gear, like carabiners, for pulleys. This is not an uncommon situation during a pickoff where you need to raise the subject a few inches to transfer his weight onto your system.
As shown in this illustration, when you attempt to lift a 200-pound subject on a 3:1 created with carabiners (which in this example have 50% friction), you will be pulling a surprising 114 lbs rather than the 67 pounds you may have expected. Your system is no longer a 3:1, or even a 2:1—it is a discouraging 1.75:1. (You can find this value in the above table, too.)
Riggers sometimes ponder where a higher-friction pulley should be placed within a mechanical advantage system to limit the effect of the friction. The answer isn't as clear as you might think. In a 3:1 system (or a 3:1 system with a change of direction pulley) it is best to put the inefficient (i.e., high-friction) pulley "furthest" from where you are pulling.
The four systems in this illustration show the effect of moving an inefficient pulley to different locations within a 3:1 system (click on the image to enlarge it).
All of the pulleys in the first system have 0% friction. This results in 3:1 mechanical advantage with the hand holding one-third (33.3 kg) of the 100 kg load.
In the second system, the friction in the pulley that is closest to the puller (the change of direction pulley) is set to 50% and the other pulleys remain at 0%. You can see that the hand must now hold twice the force!
The third system moves the high-friction pulley to the "midpoint" of the system, resulting in the hand holding 50 kg (i.e., it is a 2:1 system). The fourth system moves the high-friction pulley the furthest from the pulling hand, the optimal location, which results in the hand holding 40 kg of the 100 kg load.
This next illustration shows the effect of having one pulley with 50% friction and one pulley with 0% friction in a compound 4:1 system.
You can see that the hand is holding 33.3 kg of force regardless of the location of the pulley with 50% friction.
The next time you are rigging, don't forget to consider the effects of friction. If you are lowering a load, think about ways to increase friction which will decrease the forces you must hold: change the angle of the rope, route the rope differently (while protecting it from damage, of course), or add bars to your brake bar rack. And when raising, think about ways to decrease friction: use low-friction pulleys, use rollers or smooth edge protectors, and minimize the angle that the rope crosses other surfaces.