The "safety factor" is the ratio between the force that will be applied to a component in a system and the minimum breaking strength of the component.
To calculate the safety factor, divide the gear's minimum breaking strength by the maximum force it will support.
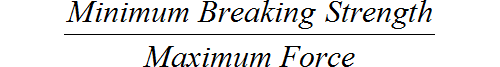
If our rope is rated at 30 kN and it is holding a 2 kN load, we can use this formula to determine that the rope has a 15:1 safety factor.
You can express the safety factor as a number (e.g., "10") or a ratio (e.g., "10:1"). If the safety factor is less than 1 it means that the force exceeds the strength and the component will fail. For example, if you hang 60 kN a 30 kN rope, the safety factor will be 0.5.
When estimating the maximum force, riggers have the option of using the maximum static force (i.e., the force when the system is motionless) or the maximum dynamic force (i.e., the forces that will be generated when a falling load is caught).
When rescuers calculate safety factors, they base the factor on static loads. This makes sense, because it is much easier to calculate static forces in the field. Rescuers ensure that the system can accommodate dynamic loads by using a sufficiently-high safety factor. For example, if a component that has a static safety factor of 10:1 encounters a dynamic event that generates forces which are five times more than expected (e.g., the litter slips over the edge and is caught by the belay line), the dynamic safety factor will be 2:1.
Each component in a rigging system has its own static safety factor (SSF). The lowest component safety factor in the entire system (i.e., the component that is most likely to fail) is the static system safety factor (SSSF).
To find the static system safety factor, start at the load and work your way through the entire system while comparing the forces to the strengths.
This next illustration shows how to calculate the safety factor of each component in a system (click to enlarge the image). The lowest component safety factor in this system is the water knot near the upper anchor. This knot has a safety factor of 5:1. Thus, the static system safety factor is 5:1.
Note that in the above example, the change of direction pulley doubles the forces generated by the 2 kN load which results in the pulley, carabiner, webbing, and anchor supporting 4 kN.
The weakest component in this system is the water knot near the upper anchor which has a SSF of 5:1. You could quickly improve the SSSF by doubling this webbing (which would increase the water knot's SSF to 10:1). The SSSF would then be 7:1 (the orange carabiner near the upper anchor). You could double this carabiner to increase the SSSF to 9:1 (the gold pulley's SSF).
Although it is often overlooked due to the relatively low forces involved, something as seemingly insignificant as the rescuer’s gripping ability can seriously affect the safety factor. A study of gripping strength found a huge range in gripping ability.
When considering safety factors, if a rescuer can only hold 30 pounds of force and the force exiting a belay device has 15 pounds of force, the system safety factor is only 2:1 regardless of the strength of the equipment.
The strength of manufactured rescue equipment is well tested and very accurate. If your gear is maintained and inspected, the only strength estimates you need to make are things that might weaken the gear (e.g., knots, a sharp edge that might cut a rope, a cross-loaded carabiner, etc).
On the other hand, the strength of the anchors that are connected to natural objects (e.g., trees, rocks, cams, pickets, etc) are very difficult to estimate. These components are usually selected on site without the opportunity for any testing. Your estimates on anchor strengths must therefore be very conservative.
If you make conservative estimates for anchors, adjust the rope strengths for knots, use adequate edge protection, and consider rope angles, your minimum strength estimates should be quite accurate (well within 30%).
The maximum force is usually more difficult to estimate than the minimum strength. You need to:
Estimating the maximum force is almost always less accurate than estimating the minimum breaking strength. If you must err, do so on the side of caution (i.e., estimate higher forces and lower breaking forces).
The optimum safety factor will ensure that the system is stronger than the forces it will encounter. Increasing the safety factor beyond this does not improve safety. And increasing the safety factor of an individual component beyond the lowest safety factor in the system does not make the system stronger.
The challenge is accurately estimating the strength of the gear, and more challenging, the maximum force the gear will encounter. More accurate estimates justify smaller safety factors. If you know the exact breaking strength and the exact load, then any dynamic safety factor greater than 1.0 is, theoretically, sufficient. If your estimates are vague, you should increase your safety factor (or much better, improve your estimates).
The dynamic safety factors used with airplanes can be as low as 1.5 (i.e., a plane can only handle 50% more than the maximum anticipated force). This low safety factor is required because airplanes are extremely weight sensitive; if aircraft were manufactured to the safety factors used in rope rescue they would never get off the ground. And because they must be light, the airline industry spends a tremendous amount of time and money to accurately determine the forces and strengths of every component.
Another consideration when determining the appropriate safety factor is the consequences of a failure. If you are hanging a lemonade sign in a tree, the consequences of a system failure is not a big deal. However, if the safety factor on your rope rescue system is inadequate and the system fails, someone may die.
If you want to increase safety, improving your ability to estimate the strengths and forces is far more important than blindly increasing the safety factor.
When all is said and done, most rescue teams use a static safety factor of between 5:1 and 15:1. The appropriate factor within that range depends your ability to accurately estimate the minimum breaking strengths and the maximum forces.
The "critical point test" (aka "scissors test") requires that if any one item fails, nobody should be injured.
A "bend" is a knot that joins two ropes.
A "hitch" is a type of knot that must be tied around another object.
The "whistle test" requires that if all rescuers let go, nobody should be injured.